R-C Circuit

An a.c. voltage,  $V=V_{\text{m}}\sin \omega t$ , is applied across a

(i) Series RC circuit in which the capacitative impedance is ‘a’ times the resistance in the circuit.

(ii) Series RL circuit in which the inductive impedance is ‘b’ times the resistance in the circuit.

Calculate the value of the power factor of the circuit in each case.

A capacitor of $50 \mu \mathrm{F}$ is in series with $100 \mathrm{\Omega }$ resistor. This branch is suddenly connected across a $100 \mathrm{V}$d.c. supply. Find 

(i) Time constant of the circuit.

(ii) Initial current.

(iii) Current equation as a function of time.

(iv) Voltage across the resistor after $6 \mathrm{ms}$.

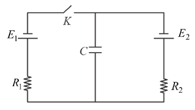
In the circuit, both the cells are ideal and $C=30 \mu \mathrm{F}, E_1=2 \mathrm{V}, R_1=3 \mathrm{\Omega }, E_2=6 \mathrm{V}, R_2=6 \mathrm{\Omega }$  and initially switch $K$ is open. At $t=0 \mathrm{s}$, the switch $K$ is closed. Long after the switch $K$ is closed, the magnitude of charge on the capacitor in steady state is

In the circuit shown in figure showing, find the energy stored in $4 \mu \mathrm{F}$ capacitor in steady state.

The time constant of the given circuit is $xRC$. Find the value of $x$.

​​​​​​​

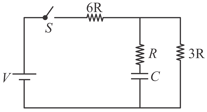
A capacitor '$C$' is connected to two equal resistance as shown in the figure. What is the ratio of time constant during charging and discharging of the capacitor?

Find heat produced on closing the switch $\mathrm{S}$

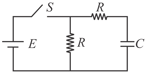
In the circuit shown the capacitor of capacitance $C$ is initially uncharged. Now the capacitor is connected in the circuit as shown. The charge passed through an imaginary circular loop parallel to the plates (also circular) and having the area equal to half of the area of the plates, in one time constant is:

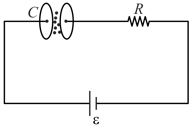
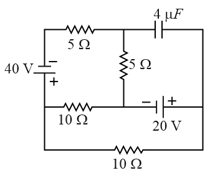
In the given figure, the charge stored in the capacitor in steady state in $\mu \mathrm{C}$ is

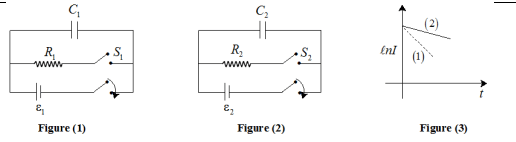
In the shown figure (1) and (2), capacitors are in the steady state. Charging batteries are removed and switches $S_1$ and $S_2$ are closed at time $t=0$. The plot of $\ln I$( $l$ is the current in the resistor) against time $t$ in the resistor $R_1$ and $R_2$ are shown by the graphs 1 and 2 respectively in the figure (3). Choose the incorrect option.

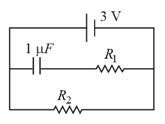
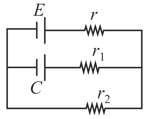
A $1 \mathrm{\mu F}$ capacitor is connected in the circuit shown below. The e.m.f. of the cell is $3 \mathrm{V}$ and internal resistance is $0.5 \mathrm{\Omega }$ . The resistors $R_1$ and $R_2$ have values $4 \mathrm{\Omega }$ and $1 \mathrm{\Omega }$ respectively. The charge on the capacitor (in $\mathrm{\mu C}$) in steady-state must be :

Charge on the capacitor when the circuit reaches steady state is

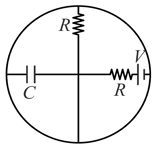
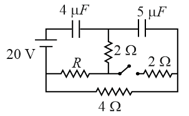
Find the potential drop across the capacitor when the circuit given below achieves steady-state.

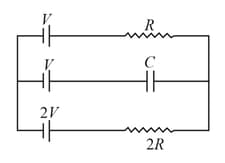
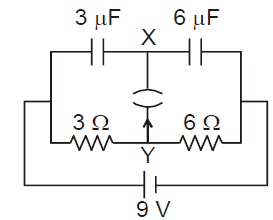
In the given circuit diagram when the current reaches steady state in the circuit, the charge on the capacitor of capacitance $C$ will be

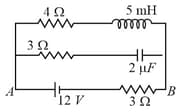
A circuit is connected as shown in the figure with the switch open. When the switch is closed, what is the total amount of charge (in $\mathrm{\mu C}$) that flows from $Y$ to $X$?

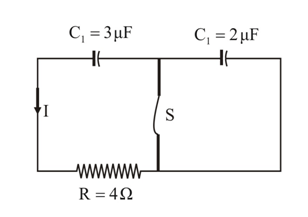
A charged capacitor $\left(C_1=3 \mathrm{\mu F}\right)$ is getting discharged in the circuit shown. When the current I was observed to be $2.5 \mathrm{A},$ switch $\text{'}S\text{'}$ was opened. Determine the amount of heat (in $\mu J$) that will be liberated in the circuit after $\text{'}S\text{'}$ is opened.

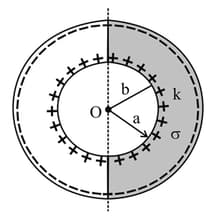
Half portion of a spherical capacitor is filled with a dielectric of dielectric constant $\mathrm{k}=2$ and conductivity $\sigma$. The charge given to spherical capacitor is ${\mathrm{Q}}_0$. Due to the conductivity of dielectric charge leaks and the time constant for the discharge circuit is $\mathrm{x}$ time of $\frac{{\epsilon }_0}{\sigma }$. Find the value of $\mathrm{x}$.

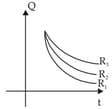
The figure shows an $\mathrm{RC}$ circuit with a parallel plate capacitor. Before switching on the circuit, plate $\mathrm{A}$ of the capacitor has a charge $-Q_0$ while plate $\mathrm{B}$ has no net charge. If at $t=0$, the switch is closed then after how much time (in seconds) will the net charge on plate A becomes zero?[Given: $C=1 \mathrm{\mu F}$, $Q_0=1 \mathrm{mC}$, $\epsilon =1000\mathrm{ }\mathrm{V}$ and $R=\frac{2\times {10}^6}{\ln 3} \mathrm{\Omega }$]

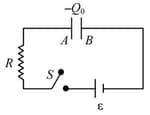
Three identical capacitor are given a charge Q each and they are allowed to discharge through resistor R₁, R₂ and R₃. Their charges as a function of time are shown in graph below. The smallest of the three resistance is:

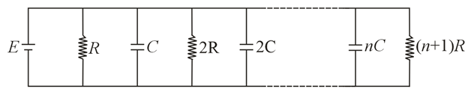
For shown situation, in steady state condition, ratio of charge stored in the first and last $n^{\mathrm{th}}$ capacitor is:-